Tìm hiểu thêm về Phần mềm thống kê Minitab
Khoảng dung sai là gì?
Dùng khoảng dung sai để tính một khoảng giá trị cho đặc tính của sản phẩm, nhằm đảm bảo một tỷ lệ nhất định sản phẩm trong tương lai đạt yêu cầu. Khoảng dung sai xác định giới hạn trên và dưới, trong đó một phần trăm nhất định của sản phẩm sẽ nằm trong giới hạn này với độ tin cậy đã cho.
Để tạo khoảng dung sai, bạn cần xác định tỷ lệ phần trăm tối thiểu của sản phẩm và mức độ tin cậy. Thường thì cả hai giá trị này gần bằng 100. Tỷ lệ phần trăm là phần trăm tối thiểu của sản phẩm bạn muốn nằm trong khoảng dung sai, còn mức độ tin cậy là khả năng khoảng dung sai sẽ thực sự bao phủ phần trăm tối thiểu đó.
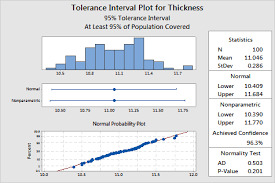 Biểu đồ khoảng dung sai trong phân tích dữ liệu
Biểu đồ khoảng dung sai trong phân tích dữ liệu
Ví dụ, một nhà sản xuất phụ tùng muốn xác định khoảng chiều rộng 99% của các bộ phận với độ tin cậy 95%, sau đó so sánh khoảng này với yêu cầu của khách hàng. Các nhà phân tích lấy ngẫu nhiên 30 bộ phận và đo chiều rộng của chúng bằng milimét (mm). Kết quả cho thấy với độ tin cậy 95%, khoảng 99% các bộ phận sẽ có chiều rộng từ 5 đến 8 mm. Nhà sản xuất tin chắc 95% rằng 99% tất cả các bộ phận sẽ nằm trong khoảng từ 5 đến 8 mm. Nếu khoảng này rộng hơn yêu cầu của khách hàng, quá trình sản xuất có thể gây ra lãng phí không cần thiết.
➤ GHI CHÚ
Phần mềm Minitab thiết lập mặc định 95% cho cả mức độ tin cậy và tỷ lệ phần trăm tối thiểu trong khoảng dung sai.
Khoảng dung sai khác với khoảng tin cậy và khoảng dự đoán như thế nào?
Khoảng tin cậy (CI), khoảng thời gian dự đoán (PI) và khoảng dung sai là các khoảng thường được sử dụng bắt nguồn từ thống kê mẫu.
Khoảng tin cậy
Phạm vi giá trị có thể chứa giá trị của một tham số tổng thể chưa biết, như giá trị trung bình, với một mức độ tin cậy nhất định.
Ví dụ: Nếu khoảng tin cậy (CI) 95% cho thể tích đổ đầy trung bình của một chai 375 ml là từ 368 đến 372 ml, bạn có thể tự tin 95% rằng giá trị trung bình thực sự của quy trình đổ đầy nằm trong khoảng này.
Khoảng dự đoán
Phạm vi giá trị cho đặc tính của sản phẩm cho thấy giá trị của một quan sát mới có khả năng nằm trong khoảng đó với một mức độ tin cậy cụ thể.
Ví dụ: Nếu khoảng dự đoán (PI) 95% cho thể tích đổ đầy trung bình của một chai 375 ml là từ 360 đến 379 ml, bạn có thể tự tin 95% rằng chai tiếp theo được lấy mẫu sẽ có thể tích đổ đầy nằm trong khoảng này.
Khoảng dung sai
Phạm vi giá trị cho đặc tính của sản phẩm có khả năng bao hàm một tỷ lệ cụ thể của tổng thể với một mức độ tin cậy nhất định.
Ví dụ: Nếu khoảng dung sai 95% cho 99% tổng thể đối với thể tích đổ đầy chai 375 ml là từ 358 đến 381 ml, bạn có thể tự tin 95% rằng 99% số chai được đổ đầy trong tương lai sẽ có thể tích nằm trong khoảng này.
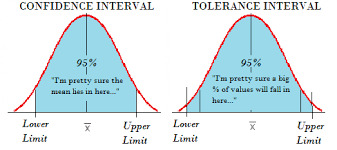 Khoảng tin cậy và khoảng dung sai
Khoảng tin cậy và khoảng dung sai
Phương pháp tham số và phi tham số
Minitab 2024 có thể tính toán khoảng dung sai bằng phương pháp tham số (ví dụ phương pháp sử dụng phân phối chuẩn) hoặc phương pháp phi tham số. Sử dụng các phương pháp phù hợp với tình huống của bạn, như sau:
Phương pháp tham số
Nếu dữ liệu của bạn theo một phân phối cụ thể, thì phương pháp tham số sẽ chính xác và hiệu quả hơn so với phương pháp phi tham số. Phương pháp tham số giúp bạn đạt được biên độ lỗi nhỏ hơn với ít quan sát hơn, miễn là phân phối bạn chọn phù hợp với dữ liệu. Hãy sử dụng phương pháp tham số nếu bạn biết từ kinh nghiệm hoặc phân tích trước đó rằng tổng thể của bạn tuân theo một phân phối đã biết.
Ví dụ, bạn có thể sử dụng kiểm tra mức độ phù hợp, một công cụ có sẵn trong Minitab qua Stat > Quality Tools > Individual Distribution Identification, để quyết định xem dữ liệu của bạn có tuân theo phân phối nào không. Nếu dữ liệu của bạn theo phân phối chuẩn, hãy sử dụng Khoảng dung sai (Phân phối chuẩn). Nếu dữ liệu của bạn theo các phân phối khác, hãy sử dụng Khoảng dung sai (Phân phối không chuẩn).
-
Lognormal
-
Gamma
-
Exponential
-
Smallest extreme value
-
Weibull
-
Largest extreme value
-
Logistic
-
Loglogistic
Phương pháp phi tham số
Các phương pháp tham số không hiệu quả nếu dữ liệu không theo một phân phối nhất định. Nếu bạn không chắc chắn về phân phối gốc hoặc biết rằng phân phối gốc không có trong Minitab, hãy sử dụng phương pháp phi tham số. Phương pháp phi tham số chỉ yêu cầu dữ liệu liên tục.
Phương pháp phi tham số thường cần cỡ mẫu lớn hơn phương pháp tham số.
Ví dụ, nếu bạn muốn bao phủ ít nhất 95% tổng thể, bạn cần khoảng 90 mẫu để khoảng dung sai chính xác. Tỷ lệ phần trăm tổng thể càng lớn, số lượng mẫu cần thiết càng nhiều.
Để xác định cỡ mẫu phù hợp cho khoảng dung sai đáp ứng mục tiêu độ chính xác của bạn, hãy chọn Stat > Power and Sample Size > Sample Size for Tolerance Intervals trong Minitab.
Ngoài ra, nếu có nhu cầu mua bản quyền Minitab chính hãng, vui lòng liên hệ ngay với Minitab Việt Nam để được nhận báo giá bản quyền Minitab và tư vấn về sản phẩm kỹ hơn:
Hotline: +84 98 332 06 55
Email: sale@.com
Website: https://minitabvietnam.com/
Add: Tầng 4, Tòa nhà N01-T4, Khu Đoàn Ngoại Giao, P. XuânTảo, Q. Bắc Từ Liêm, TP. Hà Nội
Ví dụ, một nhà sản xuất phụ tùng muốn xác định khoảng chiều rộng 99% của các bộ phận với độ tin cậy 95%, sau đó so sánh khoảng này với yêu cầu của khách hàng. Các nhà phân tích lấy ngẫu nhiên 30 bộ phận và đo chiều rộng của chúng bằng milimét (mm). Kết quả cho thấy với độ tin cậy 95%, khoảng 99% các bộ phận sẽ có chiều rộng từ 5 đến 8 mm. Nhà sản xuất tin chắc 95% rằng 99% tất cả các bộ phận sẽ nằm trong khoảng từ 5 đến 8 mm. Nếu khoảng này rộng hơn yêu cầu của khách hàng, quá trình sản xuất có thể gây ra lãng phí không cần thiết.